Cebirsel İfadelerle İşlemler (Toplama, Çıkarma, Çarpma İşlemi)
Terim, Katsayı, Benzer Terim
Cebirsel İfadelerde Toplama İşlemi
Cebirsel İfadelerde Çıkarma İşlemi
Cebirsel İfadelerde Çarpma İşlemi
CEBİRSEL İFADELER
Konuya başlamadan önce değişken, bilinmeyen nedir, cebirsel ifade nedir, katsayı nedir, terim nedir hatırlayalım.
(x, y, a gibi...) En az bir bir bilinmeyen ve bir işlem içeren ifadelere cebirsel ifadeler denir.
Bir cebirsel ifadede bir sayı ile bir veya birden fazla değişkenin çarpımına terim, değişkenle çarpım durumunda bulunan sayıya katsayı denir.
Terimleri birbirinden ayırmak için toplama ve çıkarma işlemlerinin önünden ifadeyi böleriz. Her parça bir terimdir.

Yukarıdaki örnekte olduğu gibi ifadeyi toplama ve çıkarma işlemlerinin önünden parçaladık.
Şimdi sabit terim nedir, benzer terim nedir öğrenelim.
3 terimli bu ifadede ilk terim 3x , ikinci terim +2xy , üçüncü terim ise -2'dir.
İçerisinde bilinmeyen bulunmayan terime sabit terim diyoruz.
Bir cebirsel ifadede bir değişkenin aynı veya farklı katsayılara sahip terimlerine benzer terim denir.
Örneğin: 3x / 5x / - 9x / 0,5x / x terimleri benzer terimdir.
5a / a2 / 5b / 2 / 3y terimlerinden hiç biri benzer terim değildir.
CEBİRSEL İFADELERDE TOPLAMA İŞLEMİ
Cebirsel ifadelerle toplama işlemi benzer terimler arasında yapılır.
Benzer terimlerin katsayıları arasında toplama işlemi uygulanır. (Benzer olmayan terimler toplanamaz.)
Örnek: 3x + 5x = (5+3)x = 8x (3x ve 5x benzer terim oldukları için katsayıları toplanıp 8x bulunur)
2x + 3y2 + 9x + 2y2 = 11x + 5y2 (2x ile 9x benzerdir toplanıp 11x bulunur.
3y2 ile 2y2 benzerdir toplanıp 5y2 bulunur)
CEBİRSEL İFADELERDE ÇIKARMA İŞLEMİ
Cebirsel ifadelerle çıkarma işlemi toplama işleminde olduğu gibi benzer terimlerin katsayıları arasında yapılır. Örnek: 9a - 3a = (9-3)a = 6a (9a ve 3a benzerdir.
Katsayılarını çıkartırsak 6a buluruz) 5c + 8c - 2c = (5+8-2)c = 11c (Yine benzer terimlerin katsayıları arasında toplama çıkarma işlemi yapılır.)
NOT: Burada yaptığımız toplama, çıkarma işlemine cebirsel ifadeyi sadeleştirme, veya cebirsel ifadeyi en sade halinde yazmak da denir.
Cebirsel İfadelerde Çıkarma İşlemi
Cebirsel İfadelerde Çarpma İşlemi
CEBİRSEL İFADELER
Konuya başlamadan önce değişken, bilinmeyen nedir, cebirsel ifade nedir, katsayı nedir, terim nedir hatırlayalım.
(x, y, a gibi...) En az bir bir bilinmeyen ve bir işlem içeren ifadelere cebirsel ifadeler denir.
Bir cebirsel ifadede bir sayı ile bir veya birden fazla değişkenin çarpımına terim, değişkenle çarpım durumunda bulunan sayıya katsayı denir.
Terimleri birbirinden ayırmak için toplama ve çıkarma işlemlerinin önünden ifadeyi böleriz. Her parça bir terimdir.
Yukarıdaki örnekte olduğu gibi ifadeyi toplama ve çıkarma işlemlerinin önünden parçaladık.
Şimdi sabit terim nedir, benzer terim nedir öğrenelim.
3 terimli bu ifadede ilk terim 3x , ikinci terim +2xy , üçüncü terim ise -2'dir.
İçerisinde bilinmeyen bulunmayan terime sabit terim diyoruz.
Bir cebirsel ifadede bir değişkenin aynı veya farklı katsayılara sahip terimlerine benzer terim denir.
Örneğin: 3x / 5x / - 9x / 0,5x / x terimleri benzer terimdir.
5a / a2 / 5b / 2 / 3y terimlerinden hiç biri benzer terim değildir.
CEBİRSEL İFADELERDE TOPLAMA İŞLEMİ
Cebirsel ifadelerle toplama işlemi benzer terimler arasında yapılır.
Benzer terimlerin katsayıları arasında toplama işlemi uygulanır. (Benzer olmayan terimler toplanamaz.)
Örnek: 3x + 5x = (5+3)x = 8x (3x ve 5x benzer terim oldukları için katsayıları toplanıp 8x bulunur)
2x + 3y2 + 9x + 2y2 = 11x + 5y2 (2x ile 9x benzerdir toplanıp 11x bulunur.
3y2 ile 2y2 benzerdir toplanıp 5y2 bulunur)
CEBİRSEL İFADELERDE ÇIKARMA İŞLEMİ
Cebirsel ifadelerle çıkarma işlemi toplama işleminde olduğu gibi benzer terimlerin katsayıları arasında yapılır. Örnek: 9a - 3a = (9-3)a = 6a (9a ve 3a benzerdir.
Katsayılarını çıkartırsak 6a buluruz) 5c + 8c - 2c = (5+8-2)c = 11c (Yine benzer terimlerin katsayıları arasında toplama çıkarma işlemi yapılır.)
NOT: Burada yaptığımız toplama, çıkarma işlemine cebirsel ifadeyi sadeleştirme, veya cebirsel ifadeyi en sade halinde yazmak da denir.
CEBİRSEL İFADELERDE ÇARPMA İŞLEMİ
Cebirsel ifadelerle çarpma işlemi yapılırken çarpanlardan birindeki her bir terim ile diğerindeki her bir terim ayrı ayrı çarpılır.
Elde edilen sonuçta benzer terimler varsa bunlar arasında toplama çıkarma işlemi yapılarak sadeleştirme yapılır. Cebirsel ifadelerle çarpma işlemini adım adım inceleyelim.
Bir terimli bir ifadeyle bir terimli bir ifadeyi çarpmak
Katsayılar çarpılıp katsayı olarak, bilinmeyenler çarpılıp bilinmeyen olarak sonuca yazılır.
Örnek: 3x ifadesi ile 5x ifadesini çarpalım. 3x'in katsayısı (3) ile 5x'in katsayısı (5) çarpılır. 3.5=15 3x'teki bilinmeyen (x) ile 5x'teki bilinmeyen (x) çarpılır. x.x=x2 Sonuç: 3x.5x = 15x2
Örnek: 4x ile -2y'i çarpalım.
Katsayılar çarpımı: 4.-2=-8
Biinmeyenler çarpımı: x.y = xy 4x . (-2y) = - 8xy
Bir terimli bir ifadeyle iki terimli bir ifadeyi çarpmak
Bir terimlideki terim diğer iki terimle sırayla çarpılır ve en son varsa sadeleştirme yapılır.
Örnek: 5 . ( 7x + 2y ) işlemini yapalım.
Tek terimli 5, diğer iki terimle ayrı ayrı çarpılır.
(Dağılma Özelliği gibi) = 5 . 7x + 5 . 2y = 35x + 10y
Örnek: -2x . ( x + 3 ) işleminde de aynı şekilde x ve +3'ü sırayla -2x ile çarparız. = ( -2x . x) + ( -2x . 3 ) = (- 2x2) + (- 6x)
İki terimli bir ifadeyle iki terimli bir ifadeyi çarpmak
İlk çarpandaki her bir terim ile ikinci çarpandaki her bir terim ayrı ayrı çarpılır. Sonra sadeleştirme varsa yapılır.
Örnek: ( 2x + 3 ) . ( 4x + 1 ) işlemini yapalım.
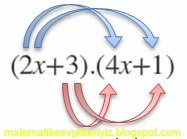
İlk ifadedeki 2x'i diğer ifadedeki 4x ve +1 ile ayrı ayrı çarpacağız.
Benzer şekilde ilk ifadedeki +3'ü diğer ifadedeki 4x ve +1 ayrı ayrı çarpacağız.
= (2x.4x) + (2x.+1) + (3.4x) + (+3.+1) = 8x2 + 2x + 12x + 3 [2x ile 12x toplanır] = 8x2 + 14x + 3
Örnek: ( x - 1 ).2 işlemini yapalım.

( x - 1 )2 = ( x - 1 ) . ( x - 1 ) demektir.
Önce ilk ifadedeki x ile diğer ifadedeki x ve -1 çarpılır.
Sonra ilk ifadedeki -1 ile diğer ifadedeki x ve -1 çarpılır.
= (x.x) + (x.-1) + (-1.x) + (-1.-1) = x2 + (-x) + (-x) + 1 [-x ile -x toplanır] = x2 -2x +1
Cebirsel İfadelerle İşlemler (Toplama, Çıkarma, Çarpma İşlemi)
 Reviewed by halis demirci
on
9.5.13
Rating:
Reviewed by halis demirci
on
9.5.13
Rating:
 Reviewed by halis demirci
on
9.5.13
Rating:
Reviewed by halis demirci
on
9.5.13
Rating:

















No comments: