Tam Sayılar (Yönlü Sayılar, Mutlak Değer, Tam Sayıları Karşılaştırma)
Tam Sayılar
Yönlü Sayılar Mutlak Değer
Tam Sayıları Karşılaştırma

Yönlü Sayılar Nedir?
Günlük hayatımızda karşılaştığımız olayların sayısal ifadelerinde doğal sayılar bazı durumlarda yetersiz kalır. Örneğin borç alma - verme, deniz seviyesinin altına inme - üstüne çıkma, kar-zarar etme gibi durumları doğal sayılarla ifade etmemiz karışıklığa sebep olur. Bu yüzden tam sayılar kümesinde yararlanılır. Tam sayılar kümesine yönlü sayılar kümesi de denilebilir. Olumlu durumlarda pozitif tam sayıları ( + ), olumsuz durumlarda ise negatif tam sayıları ( - ) kullanırız.
Örnek verecek olursak, Sıcaklık sıfırın altında 20 derece yerine -----> -20
Deniz seviyesinin 150 metre üstü -----> +150
Zemin katın altındaki 3. kat -----> -3
25 TL borç -----> -25
500 TL kâr -----> +500
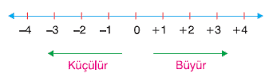
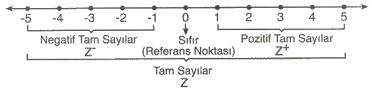
Tam Sayılar Kümesi
Yukarıda da gördüğümüz gibi sayıların önüne konulan işaretler sayının yönünü belirtir. Önünde + olan sayılara pozitif tam sayılar, - olan sayılara ise negatif tam sayılar denir.
Önünde işaret bulunmayan sayıların işareti +'dır. Sıfır sayısı ise ne pozitif ne de negatif bir tam sayıdır. Sıfıra referans noktası deriz. Çünkü sayıların pozitif mi negatif mi olduğunu sıfır ile karşılaştırarak belirleriz. Sayı doğrusunda sıfırın sağındaki sayılar pozitif, solundaki sayılar ise negatiftir.

Pozitif tam sayılar kümesi Z+ sembolü ile gösterilir. Z+ = { 1, 2, 3, 4, ...}
Negatif tam sayıalar kümesi Z- sembolü ile gösterilir.
Z- = { -1, -2, -3, -4, ...} Tam sayılar kümesi ise pozitif tam sayılar, negatif tam sayılar ve sıfırın (0) birleşiminden oluşur. Z harfi ile gösterilir.
Z = Z+ È {0} È Z- Z = { ..., -3, -2, -1, 0, 1, 2, 3, ... }
Mutlak Değer
Bir tam sayının referans noktasına yani sıfıra (0) olan uzaklığına o tam sayının mutlak değeri denir. Örneğin -5 sayısının 0'a olan uzaklığı 5 birimdir. Bu yüzden -5'in mutlak değeri 5'tir. Bu durum sembolle | -5 | = 5 şeklinde gösterilir. Sayının yanındaki çizgiler mutlak değer sembolüdür. Mutlak değer sıfıra olan uzaklık olduğu için uzaklık birimi negatif olamayacağından mutlak değer asla negatif bir sayı olamaz. 0 sayısının mutlak değeri 0'dır. Bunun dışındaki sayıların mutlak değeri pozitiftir.
| -2 | = 2 | + 5 | = 5 | 0 | = 0 | -123 | = 123
Tam Sayıları Karşılaştırma
Sayı doğrusunda sağa doğru gidildikçe sayılar büyür, sola doğru gidildikçe sayılar küçülür. Diğer bir ifade ile pozitif sayılar sıfırdan uzaklaştıkça büyür, negatif tam sayılar sıfırdan uzaklaştıkça küçülürler.

Örnekler verelim,
+5 sayısı +3 sayısının sağında olduğu için +5 > +3 -
2 sayısı -7 sayısının sağında olduğu için -2 > -7
Negatif tam sayıları karşılaştırırken borç olarak düşünmeniz karşılaştırmanızı kolaylaştıracaktır. Mesela -7 mi büyük -10 mu diye düşünelim. Sayılar negatif olduğu için -7'yi 7 TL borç, -10'u ise 10 TL borç olarak düşünebiliriz. 7 TL borç 10 TL borçtan daha iyi bir durum olduğu için -7 > -10 deriz.
Şu çıkarımlarda bulunabiliriz:
Bütün pozitif tam sayılar 0'dan büyüktür.
ütün negatif tam sayılar 0'dan küçüktür.
Herhangi bir pozitif tam sayı, bütün negatif tam sayılardan büyüktür.
Herhangi bir negatif tam sayı, bütün pozitif tam sayılardan küçüktür.
Sayı doğrusundaki bir sayı, sağındaki sayılardan küçük, solundakilerden büyüktür.
En büyük negatif tam sayı -1'dir.
En küçük pozitif tam sayı +1'dir.
Örnekler:
-15 < -29
+6 < 23
0 < 12
-23 < 0
-2 > -13
5 > -7
|-2| > -2
|-23| < 144
15 < |-18|
Tam Sayıları Karşılaştırma

Yönlü Sayılar Nedir?
Günlük hayatımızda karşılaştığımız olayların sayısal ifadelerinde doğal sayılar bazı durumlarda yetersiz kalır. Örneğin borç alma - verme, deniz seviyesinin altına inme - üstüne çıkma, kar-zarar etme gibi durumları doğal sayılarla ifade etmemiz karışıklığa sebep olur. Bu yüzden tam sayılar kümesinde yararlanılır. Tam sayılar kümesine yönlü sayılar kümesi de denilebilir. Olumlu durumlarda pozitif tam sayıları ( + ), olumsuz durumlarda ise negatif tam sayıları ( - ) kullanırız.
Örnek verecek olursak, Sıcaklık sıfırın altında 20 derece yerine -----> -20
Deniz seviyesinin 150 metre üstü -----> +150
Zemin katın altındaki 3. kat -----> -3
25 TL borç -----> -25
500 TL kâr -----> +500
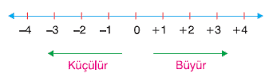
Tam Sayılar Kümesi
Yukarıda da gördüğümüz gibi sayıların önüne konulan işaretler sayının yönünü belirtir. Önünde + olan sayılara pozitif tam sayılar, - olan sayılara ise negatif tam sayılar denir.
Önünde işaret bulunmayan sayıların işareti +'dır. Sıfır sayısı ise ne pozitif ne de negatif bir tam sayıdır. Sıfıra referans noktası deriz. Çünkü sayıların pozitif mi negatif mi olduğunu sıfır ile karşılaştırarak belirleriz. Sayı doğrusunda sıfırın sağındaki sayılar pozitif, solundaki sayılar ise negatiftir.
Pozitif tam sayılar kümesi Z+ sembolü ile gösterilir. Z+ = { 1, 2, 3, 4, ...}
Negatif tam sayıalar kümesi Z- sembolü ile gösterilir.
Z- = { -1, -2, -3, -4, ...} Tam sayılar kümesi ise pozitif tam sayılar, negatif tam sayılar ve sıfırın (0) birleşiminden oluşur. Z harfi ile gösterilir.
Z = Z+ È {0} È Z- Z = { ..., -3, -2, -1, 0, 1, 2, 3, ... }

Mutlak Değer
Bir tam sayının referans noktasına yani sıfıra (0) olan uzaklığına o tam sayının mutlak değeri denir. Örneğin -5 sayısının 0'a olan uzaklığı 5 birimdir. Bu yüzden -5'in mutlak değeri 5'tir. Bu durum sembolle | -5 | = 5 şeklinde gösterilir. Sayının yanındaki çizgiler mutlak değer sembolüdür. Mutlak değer sıfıra olan uzaklık olduğu için uzaklık birimi negatif olamayacağından mutlak değer asla negatif bir sayı olamaz. 0 sayısının mutlak değeri 0'dır. Bunun dışındaki sayıların mutlak değeri pozitiftir.
| -2 | = 2 | + 5 | = 5 | 0 | = 0 | -123 | = 123
Tam Sayıları Karşılaştırma
Sayı doğrusunda sağa doğru gidildikçe sayılar büyür, sola doğru gidildikçe sayılar küçülür. Diğer bir ifade ile pozitif sayılar sıfırdan uzaklaştıkça büyür, negatif tam sayılar sıfırdan uzaklaştıkça küçülürler.

Örnekler verelim,
+5 sayısı +3 sayısının sağında olduğu için +5 > +3 -
2 sayısı -7 sayısının sağında olduğu için -2 > -7
Negatif tam sayıları karşılaştırırken borç olarak düşünmeniz karşılaştırmanızı kolaylaştıracaktır. Mesela -7 mi büyük -10 mu diye düşünelim. Sayılar negatif olduğu için -7'yi 7 TL borç, -10'u ise 10 TL borç olarak düşünebiliriz. 7 TL borç 10 TL borçtan daha iyi bir durum olduğu için -7 > -10 deriz.
Şu çıkarımlarda bulunabiliriz:
Bütün pozitif tam sayılar 0'dan büyüktür.
ütün negatif tam sayılar 0'dan küçüktür.
Herhangi bir pozitif tam sayı, bütün negatif tam sayılardan büyüktür.
Herhangi bir negatif tam sayı, bütün pozitif tam sayılardan küçüktür.
Sayı doğrusundaki bir sayı, sağındaki sayılardan küçük, solundakilerden büyüktür.
En büyük negatif tam sayı -1'dir.
En küçük pozitif tam sayı +1'dir.
Örnekler:
-15 < -29
+6 < 23
0 < 12
-23 < 0
-2 > -13
5 > -7
|-2| > -2
|-23| < 144
15 < |-18|
Tam Sayılar (Yönlü Sayılar, Mutlak Değer, Tam Sayıları Karşılaştırma)
 Reviewed by halis demirci
on
4.5.13
Rating:
Reviewed by halis demirci
on
4.5.13
Rating:
 Reviewed by halis demirci
on
4.5.13
Rating:
Reviewed by halis demirci
on
4.5.13
Rating:

















No comments: